Why light wheels matter?

Designing INCISIV

When designing Incisiv wheels, we wanted to determine the predominant factors impacting the performance.

We would like to discuss 2 of those factors on which we particularly focused: Inertia and increased relative speed at the wheels.

Power and inertia for a cyclist

For every type of cycling practise, travelling on a bike implies to fight a resistance composed of 3 distinct phenomenon: aerodynamic drag, rolling resistance proportional to weight and the change in potential energy when climbing.

To those we must add the mechanical efficiency because there are some losses through friction in the drive train. The total resistance could be defined by :

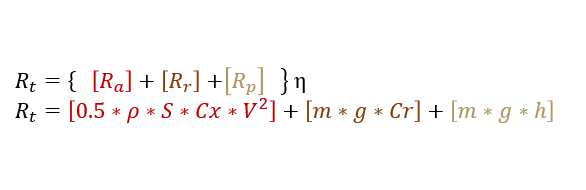
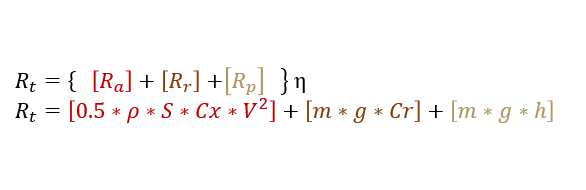
Where:

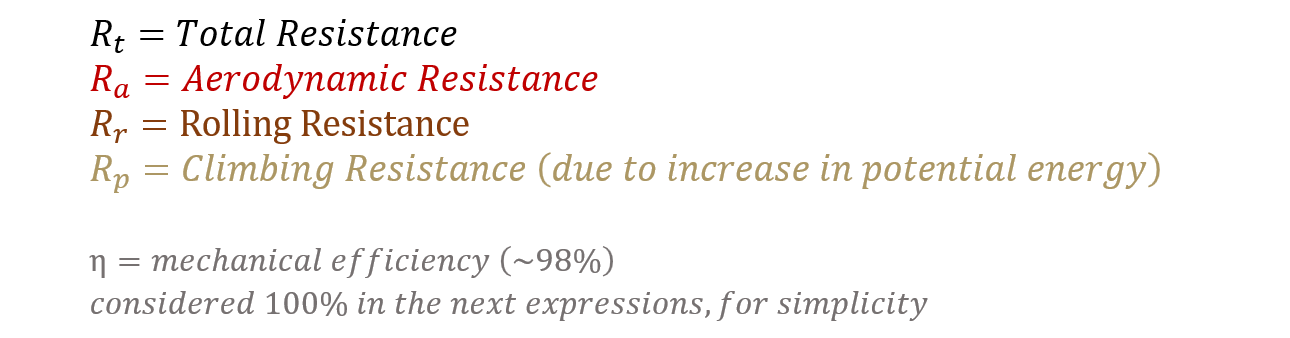
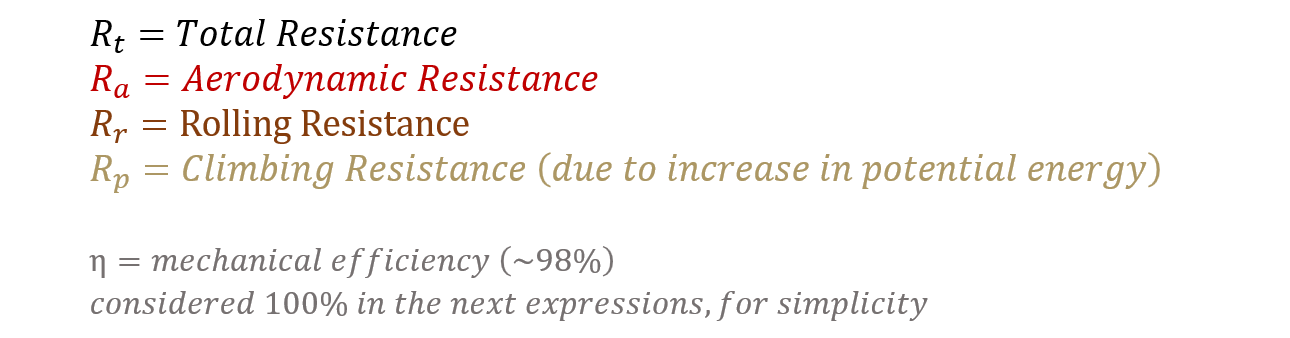
In physics, the power equals force (here the resistance) times velocity. Then, the power required by a rider to drive himself and his bike forward can be summarised by the equation:

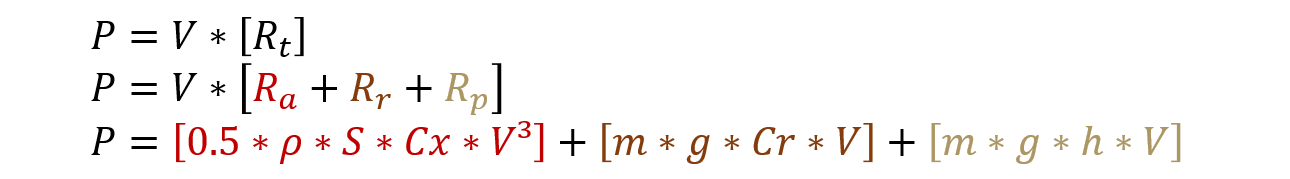
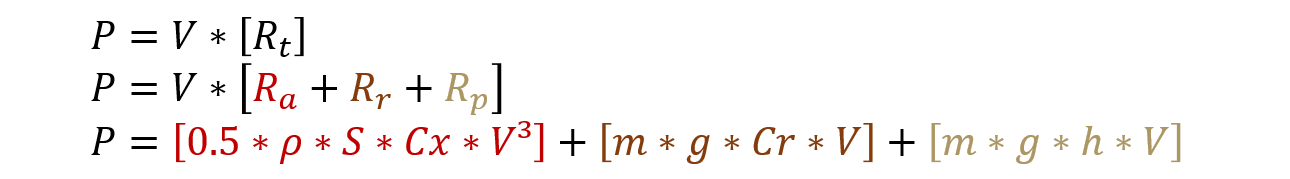
Where:

P = power
V = travel velocity
ρ = volumic mass of air
S = frontal surface
Cx = drag coefficient
m = total mass of the rider, bike, and gears
g = gravitational acceleration
Cr = rolling resistance coefficient
h = vertical height gained

Said otherwise, the required power to ride a bicycle is equivalent to the travel speed multiplied by the sum of: the aerodynamic drag, rolling resistance and climbing resistance.

For a cyclist traveling on a flat road, for example at 38km/h we can compute:

V = 38 km/h or 10.55 m/s
ρ = 1.23 kg/m³
S = 0,42 m²
Cx = 0.56
m = 75 kg (cyclist) + 7 bike = 82 kg
g = 9,81 m/s²
Cr = 0.004
h = 0 m

P = [0.5*1.23*0.42*0.56* 10.55³ ] + [82*9.81*0.004*10.55] + [82*9.81*0*10.55]
P = [170] + [34] + [0] = 204.1W
P = 204.1*η  =  204.1*0.98  =  200W

This is for a constant riding speed!

Indeed, when accelerating or decelerating a mass, according to Newton’s first law, this mass will exert a force opposing this acceleration.

For a wheel, the main portion of this opposing force is the Moment of Inertia.

Moment of Inertia

The Moment of inertia can be defined as :

Where:

I = moment of Inertia
m = mass
R = radius (distance between the moving mass and the rotating axle, here the spoke length)

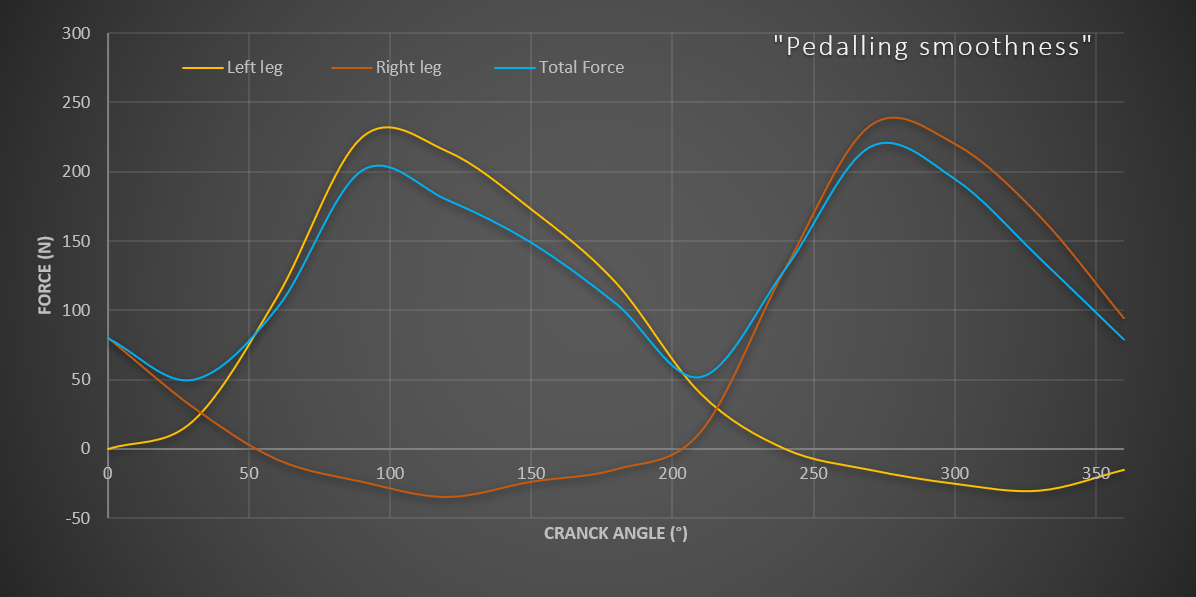
Every user of a powermeter will concur: Power is seldom constant. Of course, we constantly brake, corner, accelerate etc.

Furthermore, the power is produced by 2 legs = power is shifting from left to right at a frequency equivalent to your pedalling cadence.

The constancy of the power output of a cyclist is known as his or her ‘pedalling smoothness’.